Was ist der Korrelationskoeffizient?
Der Korrelationskoeffizient wird verwendet, um zu bestimmen, wie stark die Beziehung zwischen zwei Variablen ist, und ihre Werte können zwischen -1,0 und 1,0 liegen, wobei -1,0 eine negative Korrelation und +1,0 eine positive Beziehung darstellt. Es berücksichtigt die relativen Bewegungen in den Variablen und definiert dann, ob eine Beziehung zwischen ihnen besteht.
Korrelationskoeffizientenformel
r = n (∑xy) - ∑x ∑y / √ (n * (∑x 2 - (∑x) 2 )) * (n * (∑y 2 - (∑y) 2 ))
Wo
- r = Korrelationskoeffizient
- n = Anzahl der Beobachtungen
- x = 1 st Variable im Kontext
- y = 2 nd variablen
Erläuterung
Wenn es eine Korrelation gibt oder die Beziehung zwischen zwei Variablen sagt, muss angegeben werden, ob sich eine der Variablen im Wert ändert, dann neigt auch die andere Variable dazu, ihren Wert zu ändern, beispielsweise in bestimmten, die entweder in derselben oder in derselben sein können die andere Richtung. Der Zählerteil der Gleichung führt einen Test und die relative Stärke der Variablen durch, die sich zusammen bewegen, und der Nennerteil der Gleichung skaliert den Zähler durch Multiplizieren der Differenzen der Variablen von quadratischen Variablen.
Beispiele
Beispiel 1
Betrachten Sie die folgenden zwei Variablen, x und y. Sie müssen den Korrelationskoeffizienten berechnen.
Nachfolgend sind Daten für die Berechnung angegeben.

Lösung:
Mit der obigen Gleichung können wir Folgendes berechnen

Wir haben alle Werte in der obigen Tabelle mit n = 4.
Geben wir nun die Werte für die Berechnung des Korrelationskoeffizienten ein.

Daher ist die Berechnung wie folgt:

r = (4 · 25.032,24) - (262,55 · 317,31) / √ ((4 · 20.855,74) - (262,55) 2 ) · ((4 · 30.058,55) - (317,31) 2 )
r = 16.820,21 / 16.831,57
Der Koeffizient wird -

Koeffizient = 0,99932640
Beispiel 2
Land X ist ein wachsendes Wirtschaftsland und möchte eine unabhängige Analyse der von seiner Zentralbank getroffenen Entscheidungen in Bezug auf Zinsänderungen durchführen, ob diese die Inflation beeinflusst haben und ob die Zentralbank in der Lage ist, diese zu kontrollieren.
Nachfolgend finden Sie eine Zusammenfassung des Zinssatzes und der Inflationsrate, die im Durchschnitt des Landes für diese Jahre vorherrschten.
Nachfolgend sind Daten für die Berechnung angegeben.

Der Präsident des Landes hat sich an Sie gewandt, um eine Analyse durchzuführen und in der nächsten Sitzung eine Präsentation darüber zu halten. Verwenden Sie die Korrelation und bestimmen Sie, ob die Zentralbank ihr Ziel erreicht hat oder nicht.
Lösung:
Mit der oben diskutierten Formel können wir den Korrelationskoeffizienten berechnen. Behandlung des Zinssatzes als eine Variable, z. B. x, und Behandlung der Inflationsrate als eine andere Variable als y.

Wir haben alle Werte in der obigen Tabelle mit n = 6.
Geben wir nun die Werte für die Berechnung des Korrelationskoeffizienten ein.


r = (6 · 170,91) - (46,35 · 22,24) / √ ((6 · 361,19) - (46,35) 2 ) · ((6 · 82,74) - (22,24) 2 )
r = -5,36 / 5,88
Die Korrelation wird sein -

Korrelation = -0,92
Analyse: Es scheint, dass die Korrelation zwischen dem Zinssatz und der Inflationsrate negativ ist, was die richtige Beziehung zu sein scheint. Mit steigendem Zinssatz nimmt die Inflation ab, was bedeutet, dass sie sich tendenziell in die entgegengesetzte Richtung bewegen, und aus dem obigen Ergebnis geht hervor, dass die Zentralbank die zinspolitische Entscheidung erfolgreich umgesetzt hat.
Beispiel 3
Das ABC-Labor erforscht Größe und Alter und wollte wissen, ob zwischen ihnen ein Zusammenhang besteht. Sie haben eine Stichprobe von 1000 Personen für jede der Kategorien zusammengestellt und eine durchschnittliche Größe in dieser Gruppe ermittelt.
Nachfolgend sind Daten zur Berechnung des Korrelationskoeffizienten angegeben.

Sie müssen den Korrelationskoeffizienten berechnen und zu dem Schluss kommen, dass eine Beziehung besteht.
Lösung:
Behandeln Sie das Alter als eine Variable, z. B. x, und behandeln Sie die Höhe (in cm) als eine andere Variable als y.

Wir haben alle Werte in der obigen Tabelle mit n = 6.
Geben wir nun die Werte für die Berechnung des Korrelationskoeffizienten ein.

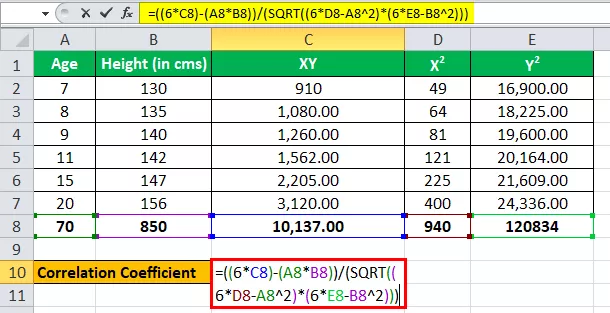
r = (6 · 10,137) - ( 70 · 850) / √ ((6 · 940 - (70) 2 ) · ((6 · 1,20,834) - (850) 2 )
r = 1.322,00 / 1.361,23
Die Korrelation wird sein -

Korrelation = 0,971177099
Relevanz und Verwendung
Es wird in der Statistik hauptsächlich verwendet, um die Stärke der Beziehung zwischen den betrachteten Variablen zu analysieren. Außerdem wird gemessen, ob zwischen den angegebenen Datensätzen eine lineare Beziehung besteht und wie gut sie in Beziehung stehen könnten. Eine der gängigen Kennzahlen für die Korrelation ist der Pearson-Korrelationskoeffizient.
Wenn sich der Wert einer Variablen und zusammen mit dieser anderen Variablen der Wert ändert, ist das Verständnis dieser Beziehung von entscheidender Bedeutung, da der Wert der ersteren Variablen verwendet werden kann, um die Wertänderung der letzteren Variablen vorherzusagen. Eine Korrelation wird heutzutage in dieser modernen Zeit vielfach verwendet, wie sie in der Finanzindustrie, in der wissenschaftlichen Forschung und wo nicht verwendet wird. Es ist jedoch wichtig zu wissen, dass die Korrelation drei Haupttypen von Beziehungen aufweist. Die erste ist eine positive Beziehung, die besagt, dass sich die zugehörige Variable in derselben Richtung ändert, wenn sich der Wert einer Variablen ändert. Wenn eine negative Beziehung besteht, verhält sich die zugehörige Variable in die entgegengesetzte Richtung. Wenn es keine Korrelation gibt, impliziert r auch einen Nullwert.Sehen Sie sich die folgenden Bilder an, um das Konzept besser zu verstehen.









