Was ist die Bereichsformel?
Die Bereichsformel bezieht sich auf die Formel, die verwendet wird, um die Differenz zwischen dem Maximalwert und dem Minimalwert des Bereichs zu berechnen, und gemäß der Formel wird der Minimalwert vom Maximalwert abgezogen, um den Bereich zu bestimmen.
Bereich = der Maximalwert - der Minimalwert
Wie vielfältig der Datensatz ist, der Statistikern und Mathematikern ein besseres Verständnis des Datensatzes vermittelt. Dies ist der einfachste Ansatz zur Berechnung der Varianz in der Statistik.
Erläuterung
Es ist recht einfach und leicht zu verwenden, da die Formel den Maximalwert abzüglich des Minimalwerts der angegebenen Stichprobe angibt. Daher ist die Varianz zwischen dem Maximalwert und dem Minimalwert der Bereich, und obwohl dies einfach zu verwenden und zu verstehen ist, muss es richtig interpretiert werden.
Wenn die Daten beispielsweise einen Outliner enthalten, wird der Bereich durch denselben beeinflusst und das Ergebnis führt zu einer falschen Darstellung. Nehmen Sie ein praktisches Beispiel für die gegebenen Daten 2, 4, 7, 7, 100, dann wäre der Bereich 100 - 2, was 98 ist, aber wie man sehen kann, liegt der Datenbereich unter 10, aber wenn man diese Daten berücksichtigt und interpretiert, liegt er innerhalb von 98 wird zu falschen Darstellungen führen. Daher sollte die Interpretation des Bereichs unter gebührender Berücksichtigung durchgeführt werden.
Beispiele
Beispiel 1
Beachten Sie den folgenden Datensatz 2,2,4,4, 4, 6,7,7,8, 8, 8, 9, 9, 9, 9, 9. Sie müssen den Bereich für diese Stichprobe berechnen.
Lösung:
- Maximalwert = 9
- Mindestwert = 2
Bereich = 9 - 2
Bereich = 7
Beispiel 2
Herr Stark, ein Wissenschaftler, der seit 10 Jahren bei einer Firma namens Dream Moon arbeitet. Herr Arora, sein Vorgesetzter, führt ein Experiment zur menschlichen Gesundheit durch und hat nur wenige Probendaten männlicher Größe gesammelt, die 162, 158, 189, 144, 151, 150, 151, 178, 155, 160 sind. Er ist jetzt und heute ratlos möchte wissen, wie viele Daten variiert werden. Herr Stark, ein erfahrener Statistiker, wurde von seinem Vorgesetzten, Herrn Arora, angesprochen, um seine Verwirrung über die Variation der Formel zu beseitigen. Herr Arora muss seinem Vorgesetzten eine Antwort geben. Sie müssen berechnen, um wie viel die Daten variieren?
Lösung:
Bereich = Maximalwert - Minimalwert
- Maximalwert = 189
- Mindestwert = 144
Bereich = 189 - 144
Bereich = 45
Die Daten oder die gesammelte Probe haben eine Variation von 45.
Beispiel 3
Herr Buffet, ein bekannter und angesehener Investor auf der ganzen Welt, erwägt derzeit US-Marktaktien und analysiert derzeit einige von ihnen, in die er investieren möchte. Die Liste enthält große Blue-Chip-Unternehmen in den USA. Nachfolgend finden Sie die angegebenen Aktien oder Wertpapiere in der engeren Auswahl sowie den aktuellen Börsenkurs, der in US-Dollar angegeben ist und in den er investieren möchte.
Sie müssen den Bereich berechnen und die Variation der Liste ermitteln.
Lösung:
Nachfolgend sind Daten zur Berechnung des Bereichs angegeben.
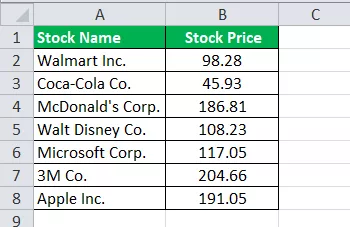
Unter Verwendung der obigen Informationen wird die Berechnung des Maximalwerts in Excel wie folgt sein:

Maximaler Wert = 204,66
Berechnung des Mindestwerts in Excel wie folgt:
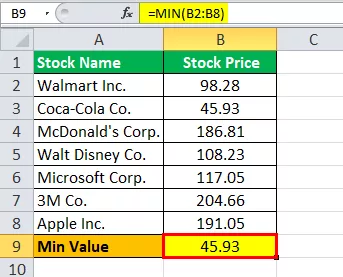
Minimaler Wert = 45,93
Daher ist die Berechnung des Bereichs wie folgt:

Bereich = 204,66 - 45,93
Die Reichweite wird -
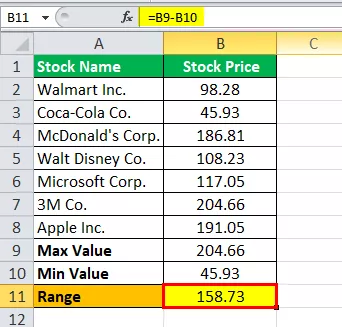
Bereich = 158,73
Verwendung der Bereichsformel
Der Bereich ist auf seine eigene Weise sehr einfach und sehr einfach zu verstehen, wie die Zahlen in dem gegebenen Datensatz oder der gegebenen Stichprobe verteilt sind, da es, wie bereits erwähnt, relativ einfach ist, die Berechnung durchzuführen, da es die gibt Dies ist nur für eine sehr einfache arithmetische Operation erforderlich, bei der nur das Minimum vom Maximalwert subtrahiert wird, für den Bereich jedoch nur wenige Anwendungen für einen bestimmten Datensatz oder eine bestimmte Stichprobe in der Statistik. Der Bereich ist auch nützlich, um ein anderes Maß für die Streuung zu schätzen, das als Varianz oder Standardabweichung bezeichnet wird.
Der Bereich kann, wie bereits erwähnt, nur über die grundlegenden Details informieren, dh wo die Streuung einer bestimmten Stichprobe oder eines bestimmten Datensatzes liegen wird. Indem Sie die Differenz angeben oder die Varianz zwischen dem höchsten und dem niedrigsten Wert einer bestimmten Stichprobe oder eines bestimmten Datensatzes angeben, erhalten Sie eine Information oder eine grobe Vorstellung von den signifikanten extremen Beobachtungen darüber, wie weit diese verteilt sind, aber auch hier gibt es keine Hinweis oder irgendeine Information bezüglich der anderen Datenpunkte, wo sie liegen würden, was die Hauptschwäche der Verwendung der Bereichsgleichung ist.
Der Bereich ist, wie oben diskutiert, nützlich, um die Streuung innerhalb einer gegebenen Probe oder eines gegebenen Datensatzes darzustellen, und wird ferner auch zum Vergleichen der resultierenden Streuung zwischen derselben gegebenen Probe oder denselben gegebenen Datensätzen verwendet.